Expectation investing
There is no monetary loss or penalty for investors who don’t make smart investing decisions in markets but there is a huge monetary loss if investors make dumb decisions in the stock market. Not making dump decisions should be investors priority rather than making smart investments decisions. One of the ways to not make dumb decisions is by making fewer decisions. Less is more in investing. Investors who try to catch every opportunity either end up making nothing or losing everything. As Warren Buffet says, you need just 3-5 ideas to become very wealthy.
Investing is the field of probabilistic science. Investors have to think in a fashion of expected value in order to make decisions. But unfortunately, humans are not wired to think in expected value terms. Investors should think into the future with a range of probabilities that could happen. In investing, the number of times you made a correct decision or number of times you made incorrect decisions is not a matter. You could have made plenty of mistakes but one single huge investments success may have made you wealthy.
Frequency Vs magnitude
The frequency of winning or losing is not important is investing but rather the magnitude with which you win or lose is important. How much money we make when we win and how much money we lose when we fail is the most important. In order to think and calculate in terms of frequency and magnitude of different outcomes, we must know how to think in expected value term.
Game of Probability
The rules of the games are, we make Rs 10 when the market goes up and we lose Rs 8 when the market goes down. The probability of market-moving down is 30%. Now, what will be the maximum amount you will be willing to pay, in order to play this game?
Answer
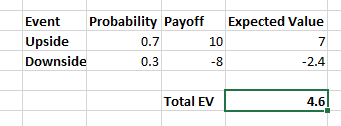
The expected monetary gain for the game is Rs 4.6. So, the maximum money one can pay to play the game is Rs 4.6. if we pay greater than Rs 4.6, then we can mathematically say that odds are not in our favor.
This most important thing we must observe is whether the odds of winning the game. If the odds are not in our favor, we can simply don’t play the game.
Expectation Thinking Example – In Pharma Industry
In pharma industry, when chemist decides to discover new generic drugs, they calculate the expected value, that is the profitability that they can get when they successfully discover that drug when they bring it to the market. Discovering new drugs requires billions of investments in research so, before they invest in research, they calculate the expected market size of the drug in the upside scenario and the maximum loss they can bear in the downside scenario (when the drug discovery fails). If the expected value(profitability) is less than the maximum loss that they can bear, they drop the research.
Thinking is an expected term in investing
We humans are inherently not designed to think in the expected term and probabilistic basis. Long term success in any probabilistic field is determined by thinking in the expected term. Since investing is a probabilistic science, investors who think in expected term has a huge edge.
Factors to be kept in mind while deciding using expected term
- Focus
If you closely observe professional gamblers, they don’t simply go into a casino and play all games but instead, they play only specific games that to only when they think that odds are in their favor. Likewise, investors should properly calculate the expected payoff from certain investments and only focus their investments where the odds are in our favor.
- Examining every possibility
Investors should examine every probable outcome that may occur. Since future events remain uncertain, we cannot focus on only single events. We must simulate various outcomes and see whether the payoff we are getting in various outcomes is favorable in our side or not.
- Magnitude of winning
Consider an event which has got a very very low probability of winning but the magnitude of payoff if we win is very huge and the downside is limited. If you apply classic expected value technique we may not participate in this event and if you decide not to participate then we are making a serious mistake. For example, consider the below scenario,
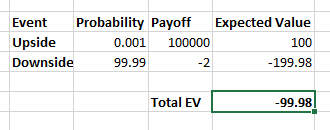
Since the expected value is negative, we may not participate in this event. It is a mistake not to participate because the magnitude of payoff is very huge and the magnitude of a downside is very limited.
When investors want to make investments where there is a low probability of success but the magnitude of payoff is huge with only limited downside, then the investor must go ahead to make those investments.

